3 Techniques for Finding the Roots of a Quadratic Equation

Finding the roots of a quadratic equation can be an important step in solving problems in a variety of fields, including mathematics, physics, and engineering. There are several techniques that can be used to find the roots of a quadratic equation, each with its own advantages and limitations.

In this blog post, we will explore three common techniques for finding the roots of a quadratic equation: factoring, using the quadratic formula, and graphing.

Factoring

Factoring is a technique that involves expressing the quadratic equation in the form of a product of two linear factors. This can be done by setting the quadratic equation equal to zero and then using the zero product property to solve for the roots.

For example, consider the quadratic equation x^2 + 4x + 4 = 0.

We can factor this equation by setting it equal to zero and then using the zero product property to solve for the roots:

Since the product of the two factors is zero, either x + 2 = 0 or x + 2 = 0. Solving each of these equations yields x = -2 as the roots of the quadratic equation.

One advantage of using factoring to find the roots of a quadratic equation is that it is often easier to do than other techniques. It is also useful for finding the roots of equations that cannot be solved using the quadratic formula (discussed below).

However, factoring can be difficult for equations that do not factor easily, and it may not be possible to use this technique for all quadratic equations.

Using the quadratic formula

The quadratic formula is a widely used technique for finding the roots of a quadratic equation. It is a formula that gives the roots of any quadratic equation in the form ax^2 + bx + c = 0, where a, b, and c are constants.

The formula is: x = (-b +/- sqrt(b^2 - 4ac)) / (2a)

To use the quadratic formula, we simply plug in the values of a, b, and c into the formula and solve for x.

For example, consider the quadratic equation x^2 - 6x + 8 = 0.

The values of a, b, and c are a = 1, b = -6, and c = 8, so we can plug these values into the formula to find the roots:

The roots of the quadratic equation are x = 4 and x = 2.

One advantage of using the quadratic formula is that it always gives the roots of a quadratic equation, regardless of whether the equation can be easily factored or not. However, it can be more time-consuming to use than factoring, and it may be more difficult for some people to remember the formula.

Graphing

Graphing is another technique that can be used to find the roots of a quadratic equation. To use this technique, we first graph the quadratic equation on a coordinate plane. The roots of the equation will be the points where the graph intersects the x-axis.

This is because at these points, the y-value of the graph will be zero (since the equation is set equal to zero), so the x-coordinates of these points represent the roots of the equation.

For example, consider the quadratic equation y = x^2 - 4x + 3.

To find the roots of this equation, we can graph it on a coordinate plane and then find the points where the graph intersects the x-axis.

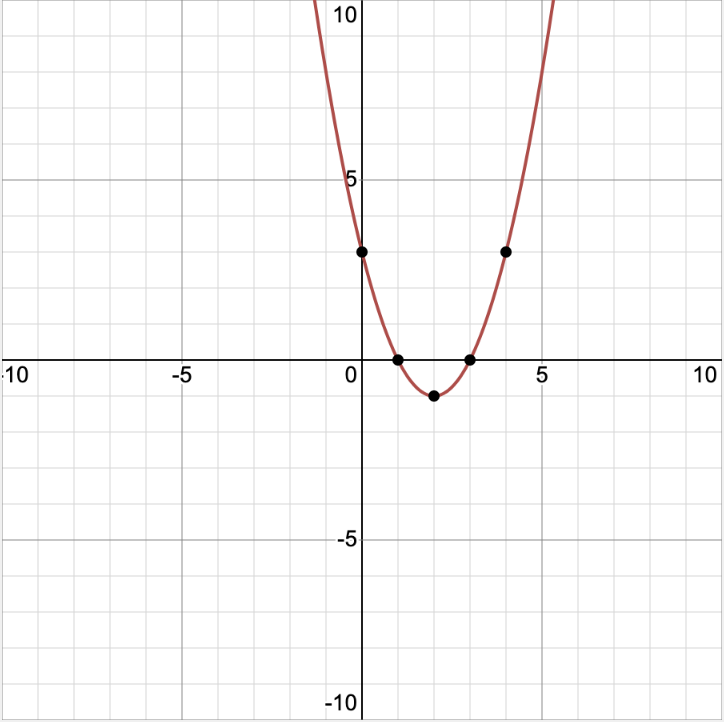
From the graph, we can see that the roots of the equation are x = 1 and x = 3.

One advantage of using graphing to find the roots of a quadratic equation is that it can be a visual and intuitive way to solve the problem. It can also be useful for finding approximate roots when an exact solution is not possible. However, graphing can be time-consuming and may not always be the most accurate method for finding the roots of a quadratic equation.

In conclusion, there are several techniques that can be used to find the roots of a quadratic equation, including factoring, using the quadratic formula, and graphing. Each technique has its own advantages and limitations, and the best method to use will depend on the specific problem at hand and the preferences of the person solving the problem.